패딩 3X3은 패딩1이 맞고 5X5는 패딩 2
디폴스는 0이다
특징지도(feature map)
– 컨볼루션 필터(직육면체) 의 적용 결과로 만들어지는 2차원 행렬
– 특징지도의 원소값
• 컨볼루션 필터에 표현된 특징을 대응되는 위치에 포함하고 있는 정도

- k개의 컨볼루션 필터를 적용하면 k의 2차원 특징지도 생성
(특징맵 나오면 다시 원위치 후 값을 다른 값으로 바꾼 후 오른쪽에서 왼쪽으로 위에서 아래로.,,k개)
그 갯수 만큼 합치게 되면 -> 직육면체
깊이의 갯수는 맵들의 갯수와 같다
풀링(pooling)
– 일정 크기의 블록을 통합하여 하나의 대푯값으로 대체하는 연산
- 최대값 풀링(max pooling)
• 지정된 블록 내의 원소들 중에서 최대값을 대푯값으로 선택
겹치면 안됨, w가 없음,특징은 살리고 , 값을 작게 하기 위해서 디폴트는2x2, 특징을 최대한 보존한다.

- 평균값 풀링(average pooling)
• 블록 내의 원소들의 평균값을 대푯값으로 사용
가중치가 없기에 학습이 안되고 그냥 값을 뽑는 용도

폴링(Pooling)이란 서브 샘플링이라고도 하는 것으로 입력 데이터의 크기를 줄이는 역할
– 컨볼루션 신경망 구조의 예
• Conv-Pool-Conv-Pool-Conv-Pool-FC-SM
• Conv-Pool-Conv-Pool-Conv-FC-FC-SM
• Conv-Pool-Conv-Pool-Conv-Conv-Conv-Pool-FC-FC-SM
• Conv-Pool-Conv-Pool-Conv-Pool-FC-FC-SM

입력해서 8개 맵(즉 직유면체), 그리고 폴링(거기서 제일 큰 값, 각 각 개별 별로 하나 뽑고 ) 일대일대응되게 각 특징별로 뽑고 그다음(conv) 폴링한 것들이 새로운 입력이 된다. 커널도 직육면체 ( 8층) 모양으로왼쪽에서 오른쪽으로 위에서 아래로
다시 복귀 후 값을 바뀌고 다시 실행 후 풀링
결과적으로 행열은 작아지고 깊이가 길어지고
그것을 fc할 때 1d로 바꿔줘야 한다 (그래야 뉴런에 입력 가능)_ 3d 가 1d로 프로그램에서 다차원을 1d로 해서 넣어준다.
합성곱 신경망 모델 실습
컨브넷 훈련하기
데이터 내려받기
- 클래스마다 1,000개의 샘플로 이루어진 훈련 세트, 클래스마다 500개의 샘플로 이루어진 검증 세트, 클래스마다 1,000개의 샘플로 이루어진 테스트 세트로 구성
- validation 처음에 경험으로 층수 설정 후 , 돌려볼 때 검증 데이터로 체크 마지막에 해보고 test / 미래 가정

레이블을 자동으로 만들어주고,

원래는 사진만 있는데 -> 카테고리화 해서 만들어주는 코드 : make_subset

모델 만들기
- Conv2D(relu 활성화 함수 사용)와 MaxPooling2D 층을 번갈아 쌓은 컨브넷으로 구성
(활성화 함수는 위에 f(y11))
- 180×180 크기(임의로 선택한 것)의 입력으로 시작해서 Flatten 층 이전에 7×7 크기의 특성 맵으로 줄어듦
- 특성 맵의 깊이는 모델에서 점진적으로 증가하지만(32에서 256까지), 특성 맵의 크기는 감소 (180×180에서 7×7까지)
(디폴트 3x3 -> 폴에서 반 줄고-> conv는 2배 늘게, 그리고 마지막은 10 언더로 맞춰야함)
(이진분류는 활성화 함수 시그모이드 쓰면 0일 때, 0.5 값이기에 더 크면 고양이 이런식으로 분류 가능)
- Rescaling 층으로 (원래 [0, 255] 범위의 값인) 이미지 입력을 [0, 1] 범위로 스케일 변환
(수치는 정규화 하고, 이미지는 리스케일층으로 0~1 사이로)
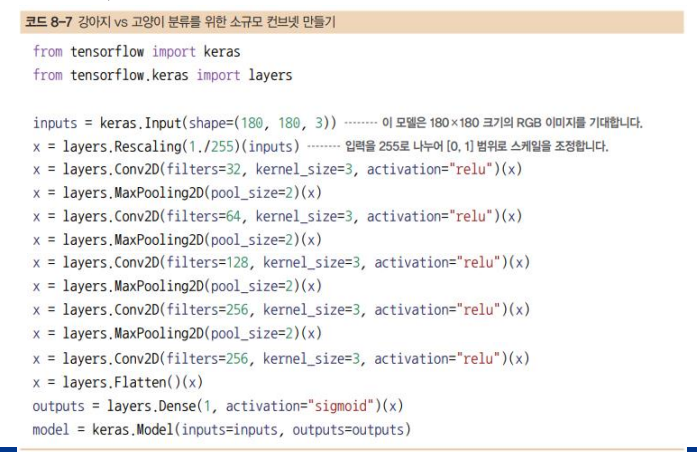
- 픽셀 하나는 (0~255) 의 값을 가지기에 255로 나누어 스케일 조정, 그리고 그 값(x)이 다시 입력으로 들어가서 출력값(x)이 다이 입력으로 들어감
(끊어지면 안됨 y로 해도 되는 데 끊어질 수 있기에 다 같은 변수x가 들어가도록)
- Dense 단층 신경망 -
180x180x3 -> 특징추출기 -> 7x7x256 -> 이것을 단층 신경망에 넣어야 한다 flatter함수를 통해 3d가 1d로 되며 들어간다.
- filter의 의미는 입력이미지가 주어지면 필터의 개수 , 그 개수만큼 특징맵이 만들어진다. kernel 사이즈는 3 3x3
poolsize는 영역의 넓이 pool을 지나면 크기가 줄기에 보상으로 필터가 두 배.필터가 너무 많으면 너무 길어서 적당한 지점까지만
- 층들을 거치면서 특성 맵의 차원이 어떻게 변하는지 살펴보자

(180,180,3)이 왜 (178,178,3)이 되냐 패딩을 안해줘서
공식!
(입력) - (커널사이즈 크기) / (스트라이드) +1 = (커널사이즈)
flatten 하지 전에 10 언더인지 확인 7x7
- 처음에 왜 4d냐 사진을 묶어서 넣어야 하기 때문에
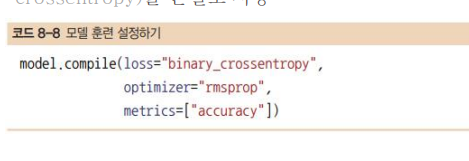
- 신경망 했었던 방법 중 하나 rmsprop방법 쓴다
데이터 전처리
- image_dataset_from_directory(directory)를 호출하면 먼저 directory의 서브디렉터리를 찾음
- 지금은 데이터가 JPEG 파일로 되어 있으므로 네트워크에 주입하려면 대략 다음 과정을 따름
1. 사진 파일을 읽음
2. JPEG 콘텐츠를 RGB 픽셀 값으로 디코딩
3. 그다음 부동 소수점 타입의 텐서로 변환
4. 동일한 크기의 이미지로 바꿈(여기에서는 180×180을 사용)
5. 배치로 묶음(하나의 배치는 32개의 이미지로 구성)
- 케라스는 이런 단계를 자동으로 처리하는 image_dataset_from_directory() 함수를 제공
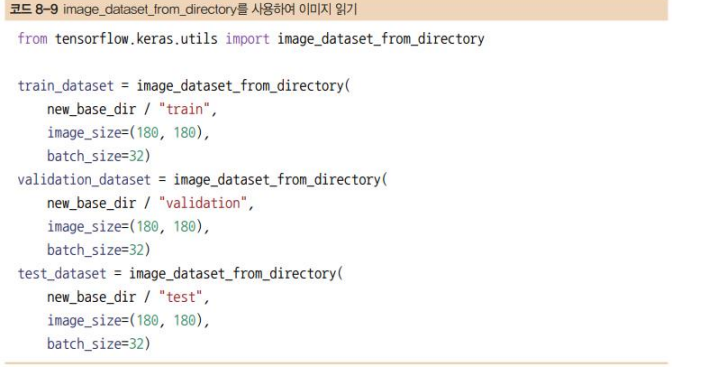
new_base_dir 은 'c:home'파일의 위치
(180,180,3) 에서 3은 생략 왜냐면 당연하니까
학습 데이터 (32, 180, 180, 3)
batch_size 는 묶음
모델 학습
- train _data에는 두 개가 들어있음(32,180,180,3), (32,) 이렇게
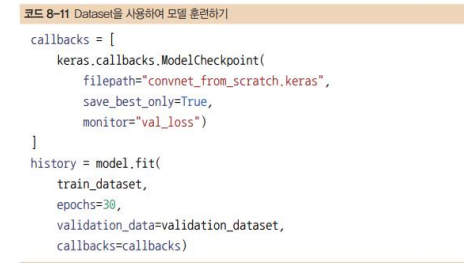
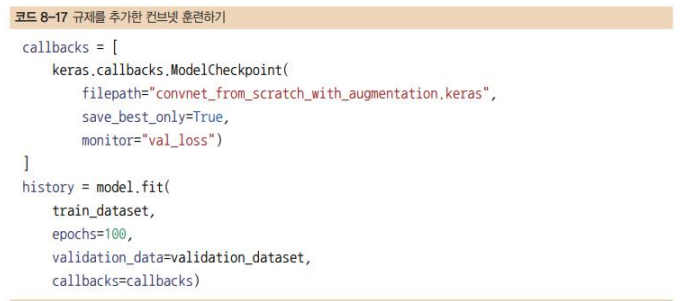
-callback은 제어할 수 있는 함수,원하는 개수만큼 컴퓨터다 알아서 오차가 작은 것을 알아서 저장
에포크 갯수 만큼
다 , monitor가 , val_loss
- 그 파일 이름은 convent_from_scratch
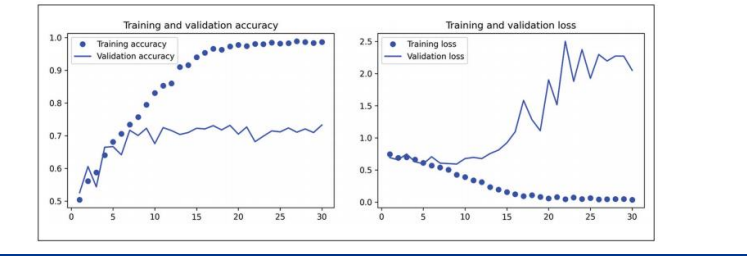
점은 시험 데이터 , 실선은 검증 데이터
과대 접합 -> 트레이닝 ,,, 이유는 샘플이 적어서다
딥러닝의 가장 기본은 학습 데이터가 많아야 한다
1) 데이터가 많아야 한다
2) 데이터 증식
3) 다음주 배울,,,
비교적 훈련 샘플의 개수(2,000개)가 적기 때문에 과대적합이 가장 중요한 문제
- 과대적합을 감소시키기 위하여, 컴퓨터 비전에 특화되어 있어 딥러닝으로 이미지를 다룰 때 매우 일반적으로 사용되는 새로운 방법인 데이터 증식을 시도해 보자
데이터 증식 사용하기
다음 Sequential 모델은 몇 개의 랜덤한 이미지 변환을 수행
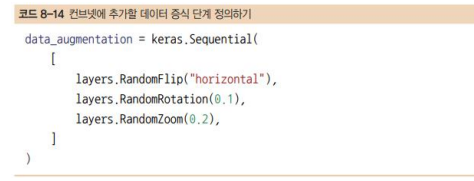
사용할 수 있는 층은 이보다 더 많음 (자세한 내용은 케라스 문서를 참고)
RandomFlip("horizontal"): 랜덤하게 50% 이미지를 수평으로 뒤집음
RandomRotation(0.1): [–10%, +10%] 범위 안에서 랜덤한 값만큼 입력 이미지를 회전(전체 원에 대한 비율이고 각도로 나타내면 [–36도, +36도]에 해당)
RandomZoom(0.2): [-20%, +20%] 범위 안에서 랜덤한 비율만큼 이미지를 확대 또는 축소
sequential은 모듈 이것을 다시 넣어줄 수 있다
- 과대적합부분을 잘라서 그 부분을 다시 학습 시킬 수 있다.
- 과대적합을 더 억제하기 위해 밀집 연결 분류기직전에 Dropout 층을 추가(강제로 뉴런은 0로)
(과대적합은 데이터는 적고 복잡할 때 일어나는 건 저명)
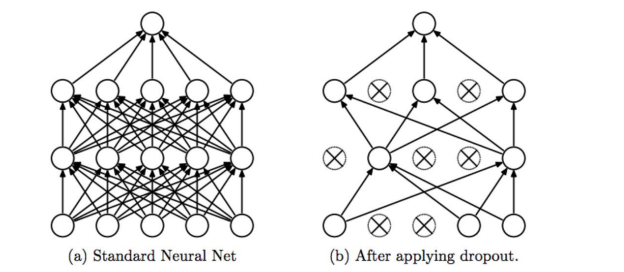
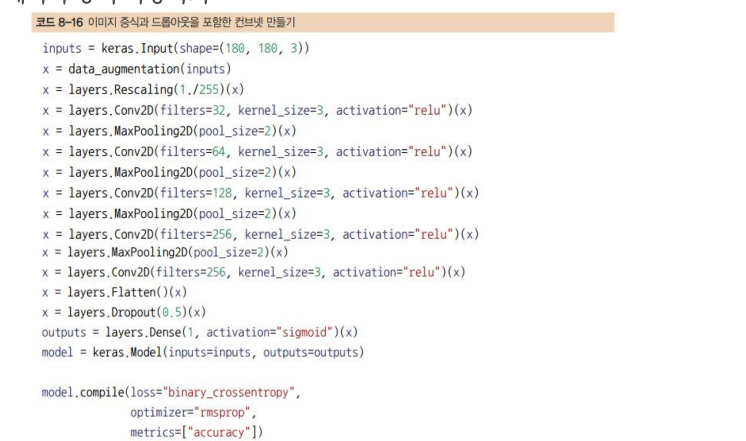
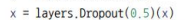
어디에 넣냐 특징추출과
주로 컨버볼류의 상위층에 넣는다, ( 주요 특징을 지울 수도 있기 때문에)
한 번 더 넣어도 됨---> 몇 개? 50프로 이상 사용하지 않는다.
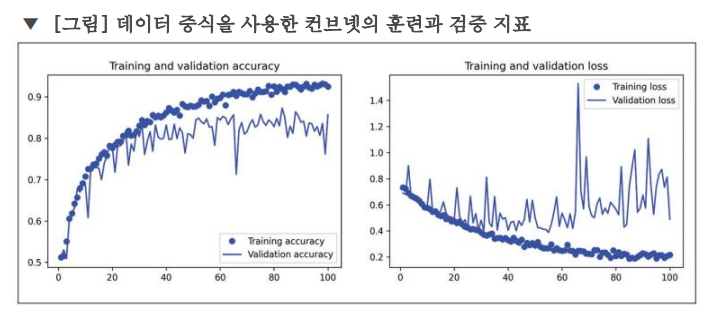
데이터 증식과 드롭아웃 덕분에 과대적합이 훨씬 늦은 60~70번째 에포크 근처에서 시작 (원본 모델은 10번째 에포크에서 시작)
- 검증 정확도는 80~85% 범위에서 유지, 이전 모델보다 훨씬 성능이 좋아졌음
'딥러닝실무응용 > 딥러닝' 카테고리의 다른 글
| [딥러닝] 전이학습(transfer learning) 및 티쳐블 머신(Teachable Machine) 실무 (0) | 2024.08.23 |
|---|---|
| [딥러닝] 합성곱신경망 코랩(Colab) 실습 (0) | 2024.08.23 |
| [딥러닝] 합성곱신경망모델(Convolution Neural Network) (0) | 2024.08.21 |
| [딥러닝] 실습(3) (0) | 2024.08.21 |
| [딥러닝] 실습(2) (0) | 2024.08.21 |



