컴퓨터 그래픽스(CG) :: 3강 기하변환(1)

목차 

1. 기본 2차원 변환

2. 동차좌표계와 기본 2차원 변환

3. 기본 3차원 변환

4. 복합 기하변환

5. 기타 기하변환

6. 좌표계 사이의 변환

7. OpenGL의 기하변환 함수

 

 

- 점의 2차원 이동변환

 

 

 

행렬로 표현하는 이유는? 컴퓨터가 행렬 빨리 계산하기 때문에 

 

2차원은 점의 이동변환이 물체의 이동 변환

 

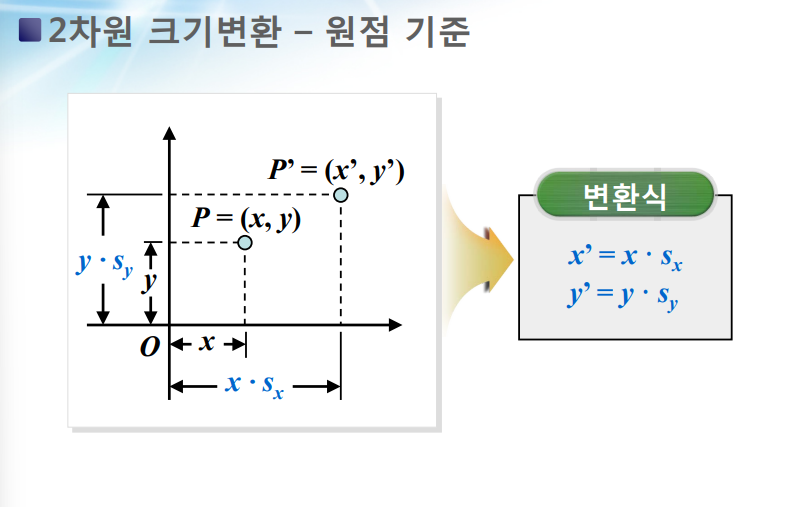
두 배가 되면 종 네 배

0.5 줄어들면 0.25 = 1/4 줄어듬

 

 

행렬 표현

 

2차원의 크기 변환은 곱으로 표현 

 

 

 

원점으로 이동 후 크기 변환 후 다시 위치 이동 시키면 된다.

 

 

2차원 회전변화 - 삼각함수 

 

 

 

 

트랜스, 스케일 ,로케이션

 

 

이렇게 컴퓨터에 계산하면 속도가 느려진다 - 왜?속도 조금만 느려져도 100만 폴리곤 처리 못함따라서 실시간성 보장이 중요한데 (실시간성 보장 : )

 

100만 폴리곤 처리 (최소 점 200만개)1초당 100만개의 폴리건 처리  (여기서 처리 후  렌더링 등등)    초당 30fps 가 매끄럽 / 100만 폴리건 처리 못해서 15fps 는 끊겨서 보일 수 있음

 

한 폴리건은 최소 점 세 개를 가짐

 

 

다각형은 무한개  삼각형은 무조건 어떤 경우에도 한 평면에 있다( 사각형은 평면이 아닐 수 있다.)

 

행렬의 곱과 합이 같이 들어가면(중간에 덧셈이 들어가면) 속도가 급격히 느려짐

 

그래서 그래픽스에서 찾아냄  

 

 

동차좌표계 ( homogeneous coordinate)

 

2차원 은 데카르트 좌표계

동차좌표계의 정의 ( x,y,h),h!=0

 

행렬 덧셈을 다 곱셈으로 만들 수 있음

 

 

 

세 점은 같은 점이다

 

 

 

 

다 곱을 나타내어 컴퓨터에 계산이 빨라지고 느려질 일이 없다

 

 

 

3차원의 이동변환

 

 

 

 

 

 

 

 

3차원 크기변환

 

 

 

 

 

3차원의 회전변환

 

 

 

 

z축 기준

x축 기준

y축 기준