분류
선형회귀
: 1차원 방정식 상에서 예측
- 입력 데이터의 특징들이 선형 조합의 특성을 갖은 회귀 학습 알고리즘 모델
- 입력 데이터들을 이용하여 데이터들을 가장 잘 설명할 수 있는 직선(linear)을 찾는 방법
종속 변수 : 어떤 입력 값의 영향을 받아서 변화하는 변수
독립 변수 : 다른 변수에 영향을 받지 않고 종속 변수에 영향을 주는 변수
회귀(Regression)와 분류(Classfication)
목표 : 우리가 학습한 데이터를 통계로 어떤 임의의 점이 평면 상에 그려졌을 때 최적의 선형 모델을 찾는 것
선형회귀(Linear Regression)의 학습/추론 과정
▪ 레이블이 있는 데이터 집합: 을 가지고 있다 가정
▪ N: 데이터 집합의 크기(개수), xi: i = 1, . . . , N의 특징 벡터, yi: 실제 타겟 값
▪ 입력 데이터 x에 대하여 특징들의 선형 조합으로 fw,b(x) 모델을 생성
▪ fw,b(x) = WX + b ▪ W: 파라미터 벡터(기울기, weight), b: 실제 값(절편, intercept)
▪ 알고리즘 학습의 높은 정확도를 위해서는 최적의 W, b 값을 찾는 것이 중요
파라미터 / 하이퍼파라미터 정해지지 않은 값 ; 기가 찾는ㄱ ㅓ 파라미터는 최적의 W,b 값을
하이퍼파라미터 : 초인자, 사용자가 정하는 파라미터 .기준이 없다 / 알려진 것들이 좀 있다

선형 회귀의 해
▪ Solution
▪ 선형 회귀의 hyperplane(초평면, 해집합)은 모든 학습 데이터에 최대한 가까워지는 위치의 직선이 선택됨
▪ 비용함수(Cost function)의 결과값이 최소가 되는 최적의 값(w∗와 b∗)을 구해야 함
▪ cost function, loss function
▪ 손실함수(Loss function)는 i번째 데이터에 대해서 실제값과 예측값의 차이 로 오류의 정도를 나타냄
▪ 모든 모델 기반 학습 알고리즘들은 손실함수를 가짐
-오차 최소화 시키기
오차값은 선형회귀 예측값과 실제값 비교
처음 w,b 레이블은 있음 x값만 넣고 실제 값과 비교 한 것이 손실함수
손실함수
두 점 사이의 차
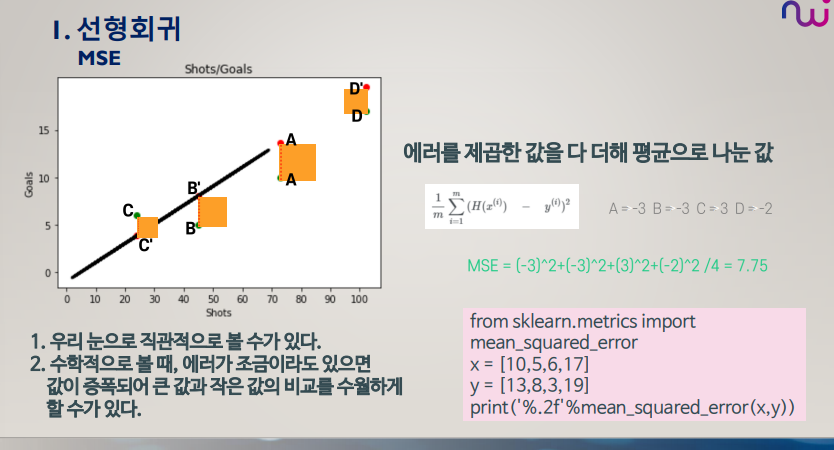
▪ 평균 제곱 오차(MSE: Mean Squared Error)
▪ + 혹은 – 방향을 고려하지 않고 양수/음수 관계 없이 동일하게 반영되도록 모든 손실에 제곱
▪ 평균 절대 오차(MAE: Mean Absolute Error)
▪ Huber Loss: MSE와 MAE 절충 방법
▪ Coefficient of Determination: 1−MSE/VAR으로 구하는 결정 계수
손실함수도 채택하는 것도 우리가 선택 -> 자동으로
예시 ) 라리가에서 뛰는 4명의 선수가 각각 이번시즌에 73,45,24,102개의 슈팅을 시도했다면 그 중 몇 골을 넣을까?


MSE (평균 제곱 오차)
제곱을 하는 이유는 값을 증폭시켜 눈으로 더 잘보이게 함
[: ,0:1] 전체에서 0에서 1번째
regr.fit(,) ---fit은 학습 데이터
regr.coef _ 가충지
선형회귀 예제
| fit(self, X, y[, sample_weight]) | 선형 모델에 적합(훈련)하기 |
| get_params (self[, deep]) | 파라미터 값 획득 |
| predict(self, X) | 선형모델을 사용하여 예측 |
| score(self, X, y[, sample_weight]) | 예측에 대한 결정계수(coefficient of determination)의 정확도 반환 |
| set_params(self, \*\*params) | 파라미터 값 설정 |
weathe = weather.drop 몇 개만 빼
'머신러닝 > 머신러닝 실무' 카테고리의 다른 글
| [머신러닝] 학습 알고리즘 최적화 (0) | 2024.09.13 |
|---|---|
| [머신러닝] 10주차 학습 알고리즘 최적화 : 경사하강법(Gradient Descent) (0) | 2024.08.22 |
| 5주차 머신러닝 :: Support Vector Machine(SVM) (0) | 2024.08.09 |
| 3주차 머신러닝 데이터 시각화 (1) | 2024.08.05 |
| 2주차 - 머신러닝 데이터분석 :: 판다스(Pandas) (0) | 2024.08.02 |



