학습 정확도
검증 정확도
예측 정확도 - 예측이 잘되었는지도 확인
보통 8:2 . 8:1:1
7:3 7:1.5:1.5
경사하강법 (Gradient Descent)
▪ 함수의 최소값을 찾는 반복적인 최적화 알고리즘
(곡선의 꼭짓점 찾기 = 기울기 0인 곳)
▪ 경사 하강을 이용하여 함수의 최소값을 찾는 방법
▪임의의 지점에서 시작하여 기울기의 음수에 비례하도록 움직임
▪ linear regression, logistic regression, SVM and neural network을 위한 최적화된 파라미터를 찾음
손실함수
- 실제값과 예측값의 차이를 구하는 함수
▪ 오차와 손실함수는 비례 관계
▪ 머신러닝 학습에서 손실함수 값을 최소화하는 파라미터(W, b)를 찾는 것이 목표
▪ 손실함수의 값을 최소화하기 위해 경사하강법 사용
▪ 평균제곱근(MSE, mean squared error)사용

비선형일 때 미분하여 기울기를 줄이며 최적의 해 찾음
▪ 기울기가 0일 때의 값을 사용(local minima)
가장 작은 꼭짓점일지 가장 큰 꼭짓점인지 모름 -> 따라서 오래 걸림 그래서 보통 제일 먼저 찾는 점을 답으로 한다
글로벌 미니마가 아닌 제대로 찾지 못한 로컬 미니마

▪ 비선형에서 많이 사용
▪ 2차원 이상의 곡선을 미분하여 경사(기울기)가 최소가 되는 점을 찾음
▪ 기울기가 0일 때의 값 사용(최소점)

▪ 데이터가 많으면, Global minima에 도달하기 까지 시간이 오래 걸림 (전체 훈련 세트 사용)
▪ Local minima에 빠지면 나오기 어려움

▪ 학습률 설정에 따라 Global minimum에 수렴하는 속도가 너무 느리거나, 학습 간격이 너무 넓어서 훈련데이터를 제대로 학습하지 못할 수 있음
▪ 학습률(Learning Rate): 훈련 데이터 학습 간격 설정 0.0001 ~ 0.1 ( 하이퍼 파라미터 ,개발자가 정하는 임의의 값)
경사하강법(Gradient Descent) 학습방법
선형 회귀 모델 : f(x) = wx + b

반복(epoch) 수행
▪ 1회 반복(epoch)마다 각 파라미터를 전체 훈련데이터 세트로 업데이트 함
▪ 첫번째 (epoch): w ← 0, b ← 0
▪ 1회 반복(epoch)마다 편미분 수행
- 학습률 = α






1000번 반복

2500번 반복해서 에러가 234-> 0 으로 줌

100번과 2500 번의 오류차가 별로 나지 않아서 100번이 최적이라고 볼 수 있다.
확률적 경사하강법(Stochastic Gradient Descent:SGD)
경사하강법 보완하는 방법
SGD 학습에서는 각 샘플 데이터에 따라 가중치 갱신
▪ 잦은 가중치 갱신으로 수렴 시간이 오래 걸릴 가능성이 있음
▪ 잦은 가중치 갱신으로 local minima에서 갇혔을 때 빠져나올 가능성이 높음
- 전체 데이터를 나눈다

▪ 미니 배치를 이용
▪ 매 스텝에서 1개의 배치를 무작위로 선택 후 gradient를 계산하여 Global Minima를 찾음
▪ 순차적으로 데이터의 기울기를 계산하지 않고, 미니 배치를 이용하여 학습
▪ 학습 단계 마다 배치가 변경되어 결과의 진폭이 크지만, 속도가 매우 빠름
▪ 일반적으로 데이터가 많으면 최적화에 오래 걸림
▪ 그러나 SGD는 미니배치를 이용, 학습속도가 매우 빠르다!
▪ SGD Classifier와 Regressor
SGDClassifier
▪ 분류에 대한 다양한 손실 함수 및 패널티를 지원하는 확률적 경사하강법
손실 파라미터
▪ loss="hinge": (소프트마진) 선형 SVM
▪ loss="modified_huber": smoothed hinge loss
▪ loss="log": 로지스틱 회귀
- 세 가지 중 괜찮은 것을 찾아내야한다.
패널티 파라미터(= regularization, 정규화: 과대적합을 예방하고 성능을 높임)
normalizaition, standardzation,regularization 셋 다 다름
penalty="L2": Ridge
▪ 손실함수에 가중치에 대한 제곱을 더하는 방법(가장 많이 사용)
▪ 변수 간 상관성 때문에 실제로 사용할 수 있는 정보가 적을 경우
▪ 독립 변수 간의 편차를 줄이기 위해 사용
penalty="L1": Lasso
▪ 손실함수에 가중치의 절대값을 더해주는 방법
▪ 변수가 무수히 많은 경우, 관련성이 작은 변수들의 계수를 0으로 만들어
▪ 영향력 있는 변수들만 남겨놓는 방법(버린 것들이 영향력이 큰 변수들이라면 L2 사용)
▪ 중요 변수만 사용하여 해석력이 강하지만, 정보의 손실과 정확도의 감소가 발생
penalty="Elastic Net"
▪ L1, L2 혼합형
▪ 큰 데이터 세트에서 작동, Ridge와 Lasso의 장점을 모두 가짐
▪ 편차와 변수 수를 줄임
SGD Classification 이해 및 실습
코랩 실습 진행



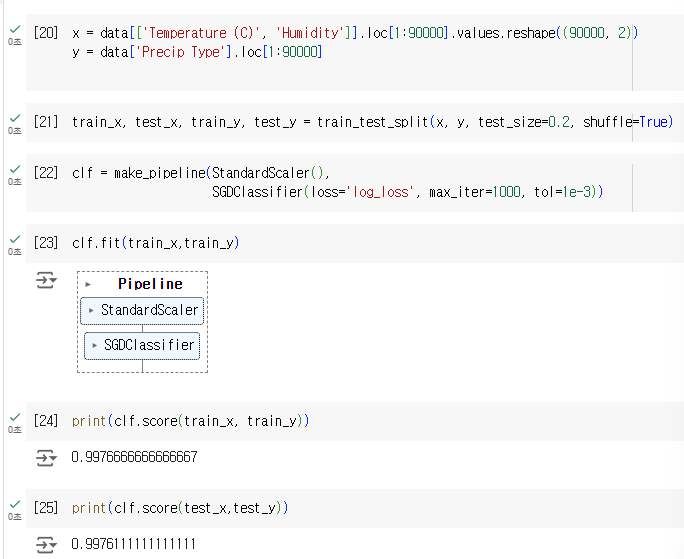



위의 내용 실행 시작부터의 시작
SGD Regression
▪ Feature Scaling을 위한 전처리 방법으로 Feature Scaling에 민감한 모델이나
데이터의 최소, 최대값을 모르는 경우나 데이터 크기의 편차가 큰 경우에 사용

▪ 선형 회귀 모델에 맞게 다양한 손실 함수와 패널티를 지원하는 확률적 경사하강법
▪ 일반적으로 대용량 데이터(10000개 이상)의 회귀문제에 적합
▪ 다른 경우(10000개 이하): Ridge, Lasso, ElasticNet 추천
-빅데이터란 만 개이상의 데이터 즉 sgd는 만 개 이상일 때에만
MSE 제곱 - 값을 크게
MAE 루트
손실 파라미터
loss="squared_loss"
▪ 보통의 최소 제곱 방법
loss="huber"
▪ 모든 지점에서 미분가능하며, Outlier에 강함
▪ MSE와 MAE를 절충한 손실함수
loss="epsilon_insensitive"
▪ epsilon보다 작은 오류에 무관한 손실함수
▪ 선형 Support Vector Regression에 사용
epsilon(𝜖)
▪ 오류에 대한 페널티가 주어지지 않는 허용 한계
alpha
▪ 정규화 항을 곱하는 상수
▪ 값이 높을수록 정규화가 강해짐
▪ 기본값=0.0001
toi
▪ 미세 조정값
SGD Regression 이해 및 실습
▪ 콘크리트 강도를 예측하기 위한 예제
▪ 총 1030개의 데이터
s








학습 알고리즘의 특수성에 따른 선택
범주형 feature 적용 가능한 경우: Decision Tree / SVM / Logistic & Linear Regression / KNN
변주형 변수 (순서에 상관없이 두가지 이상의 그룹으로 나눌 수 있는 변수) ex) 색상 변수 = 빨간색, 노란색, 초록색
각 클래스에 가중치 적용 가능: SVM
데이터의 비중이 다르거나 중요도가 다를 때 적용
오직 주어진 feature vector에 의해서만 클래스 출력하는 경우: SVM / KNN
SVM: 집합 군 사이의 Support Vector에 의한 결정 경계로 클래스 분류
KNN: k개의 이웃 탐색 후 가장 많은 feature의 target으로 클래스 분류
정답에 가까울 확률(%)로 표현 0과 1사이의 값으로 반환 가능한 경우 : Logistic regression / Decision Tree
한번에 전체 데이터 집합을 사용해 모델을 학습하는 경우 : Decision Tree / Logistic regression / SVM classification
미니 배치로 나눈 후 한 번에 한 배치씩 반복적으로 학습하는 경우 : Naïve Bayes / Multilayer Perceptron / SGD Classifier / SGD Regressor / PassiveAgressive Classifier / PassiveAgressive Regressor
classification 과 regression 모두 사용가능한 경우 : DECISION TREE / SVM / KNN
Decision Tree와 KNN: Classification을 더 많이 사용
SVM: Regression과 Classification 모두 사용
'머신러닝 > 머신러닝 실무' 카테고리의 다른 글
| [머신러닝] 학습 알고리즘 최적화 (0) | 2024.09.13 |
|---|---|
| 4주차 머신러닝 :: 선형회귀 (0) | 2024.08.10 |
| 5주차 머신러닝 :: Support Vector Machine(SVM) (0) | 2024.08.09 |
| 3주차 머신러닝 데이터 시각화 (1) | 2024.08.05 |
| 2주차 - 머신러닝 데이터분석 :: 판다스(Pandas) (0) | 2024.08.02 |



