1. 경사하강법(Gradient Descent)의 이해
2. 확률적 경사하강법(Stochastic Gradient Descent: SGD)과 SGD Classification 이해 및 실습
3. SGD Regression 이해 및 실습
2. SGDClassifier
▪ 분류에 대한 다양한 손실 함수 및 패널티를 지원하는 확률적 경사하강법
- 손실 파라미터
▪ loss="hinge": (소프트마진) 선형 SVM
▪ loss="modified_huber": smoothed hinge loss
▪ loss="log_loss": 로지스틱 회귀
- 패널티 파라미터(= regularization, 정규화: 과대적합을 예방하고 성능을 높임)
- penalty="L2": Ridge
▪ 손실함수에 가중치에 대한 제곱을 더하는 방법(가장 많이 사용)
▪ 변수 간 상관성 때문에 실제로 사용할 수 있는 정보가 적을 경우
▪ 독립 변수 간의 편차를 줄이기 위해 사용
- penalty="L1": Lasso
▪ 손실함수에 가중치의 절대값을 더해주는 방법
▪ 변수가 무수히 많은 경우, 관련성이 작은 변수들의 계수를 0으로 만들어
▪ 영향력 있는 변수들만 남겨놓는 방법
▪ 중요 변수만 사용하여 해석력이 강하지만, 정보의 손실과 정확도의 감소가 발생
- penalty="Elastic Net"
▪ L1, L2 혼합형
▪ 큰 데이터 세트에서 작동, Ridge와 Lasso의 장점을 모두 가짐
▪ 편차와 변수 수를 줄임
실습 예제



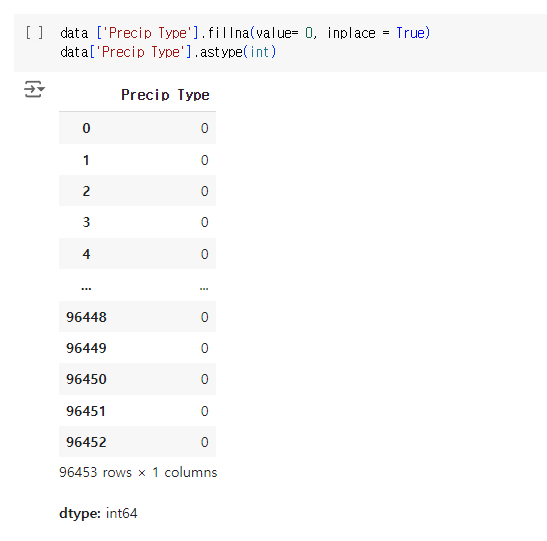




SGD Regression
▪ Feature Scaling을 위한 전처리 방법으로 Feature Scaling에 민감한 모델이나 데이터의 최소, 최대값을 모르는 경우나 데이터 크기의 편차가 큰 경우에 사용
특징
▪ 다차원의 값을 비교 분석하기 쉽게 만듦
▪ 데이터의 Overflow 및 Underflow 방지
▪ 이상치가 존재하는 경우 균형 있는 스케일링이 되지 않음
방법
▪ 각 feature의 평균을 0, 분산을 1로 변경
▪ 입력 벡터 속성을 [0,1] 혹은 [-1,1]로 스케일링

SGDRegressor
▪ 선형 회귀 모델에 맞게 다양한 손실 함수와 패널티를 지원하는 확률적 경사하강법
▪ 일반적으로 대용량 데이터(10000개 이상)의 회귀문제에 적합
- 다른 경우(10000개 이하): Ridge, Lasso, ElasticNet 추천
▪ 손실 파라미터
▪ loss="squared_loss"
- 보통의 최소 제곱 방법
▪ loss="huber"
- 모든 지점에서 미분가능하며, Outlier에 강함
- MSE와 MAE를 절충한 손실함수
▪ loss="epsilon_insensitive"
- epsilon보다 작은 오류에 무관한 손실함수
- 선형 Support Vector Regression에 사용
▪ epsilon(𝜖)
▪오류에 대한 페널티가 주어지지 않는 허용 한계
▪ alpha
▪ 정규화 항을 곱하는 상수
▪ 값이 높을수록 정규화가 강해짐
▪ 기본값=0.0001
▪ toi
▪ 미세 조정값
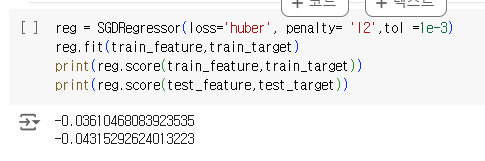
실습









'머신러닝 > 머신러닝 실무' 카테고리의 다른 글
| [머신러닝] 10주차 학습 알고리즘 최적화 : 경사하강법(Gradient Descent) (0) | 2024.08.22 |
|---|---|
| 4주차 머신러닝 :: 선형회귀 (0) | 2024.08.10 |
| 5주차 머신러닝 :: Support Vector Machine(SVM) (0) | 2024.08.09 |
| 3주차 머신러닝 데이터 시각화 (1) | 2024.08.05 |
| 2주차 - 머신러닝 데이터분석 :: 판다스(Pandas) (0) | 2024.08.02 |



